机器学习：逻辑回归

.

参考资料

  1. Logistic回归公式推导和代码实现
  2. Python:使用UCI葡萄酒数据集进行分类练习
  3. How to use .data files from UCI
  4. 优化算法使用总结——0.618法、梯度下降、牛顿法、共轭梯度、外罚、内罚
  5. 最优化方法复习笔记（六）共轭梯度法
  6. 共轭梯度法（二）：非线性共轭梯度
  7. 数值优化（4）——非线性共轭梯度法，信赖域法 ⭐实现
  8. logistic回归与牛顿法
  9. 如何通过牛顿方法解决Logistic回归问题
  10. 最优化算法之共轭梯度法
  11. AI之旅（5）：正则化与牛顿方法
  12. 共轭梯度法详细推导分析
  13. 逻辑回归、优化算法和正则化的幕后细节补充

β计算公式

遇到的问题

  1. 当我想要更改UCI数据集预测的阈值时发现不成功，无论怎么修改都是一样的结果：
1
2
GD_y_predict = sigmoid(GD) > 0.5  # 修改成0.6、0.7一样
NT_y_predict = sigmoid(NT) > 0.5

打印sigmoid(GD)发现结果已经全部是1和0了，不是我想象中0.36、0.78这样的概率值，考虑应该是theta太大，导致 X @ theta值要么很大要么很小，而sigmoid函数在输入超出[-5,5]区间时已经是接近了极限0/1。

1
2
3
4
print(GD_theta)
print(NT_theta)
------------------

解决这个方法最直接想到的就是要减小theta的值，通过在拟合多项式曲线的时候知道当模型很复杂，过拟合的情况下会出现theta绝对值很大的情况，初步考虑是需要增大正则项的系数，控制theta的大小。

1
2
GD_theta = gradient_descent(poly_X(x_train,1,4),y_train,iterations=100000,lamb=0.3)
NT_theta = newton_method(poly_X(x_train,1,4),y_train,iterations=10000,lamb=0.3)

通过对两种方法尝试不同的lambda值，得到结果：

牛顿法

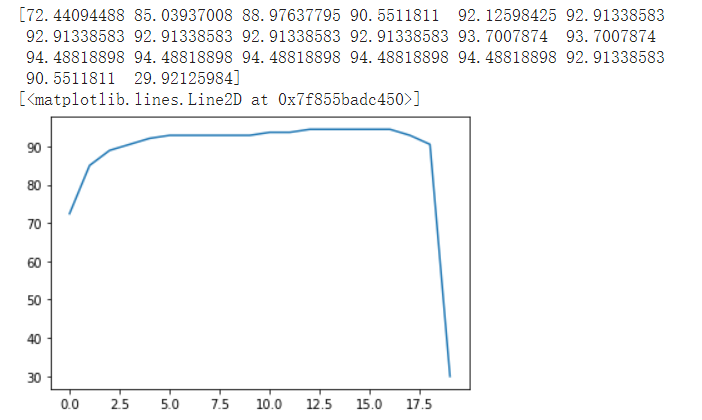
image-20211019192812327

梯度下降法

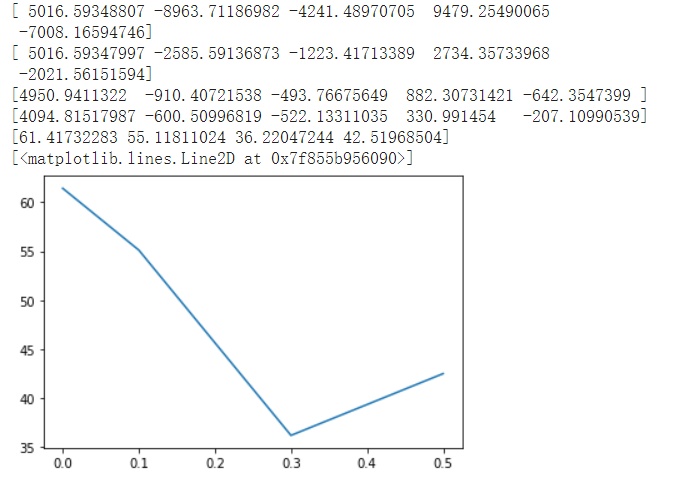
image-20211019210633842

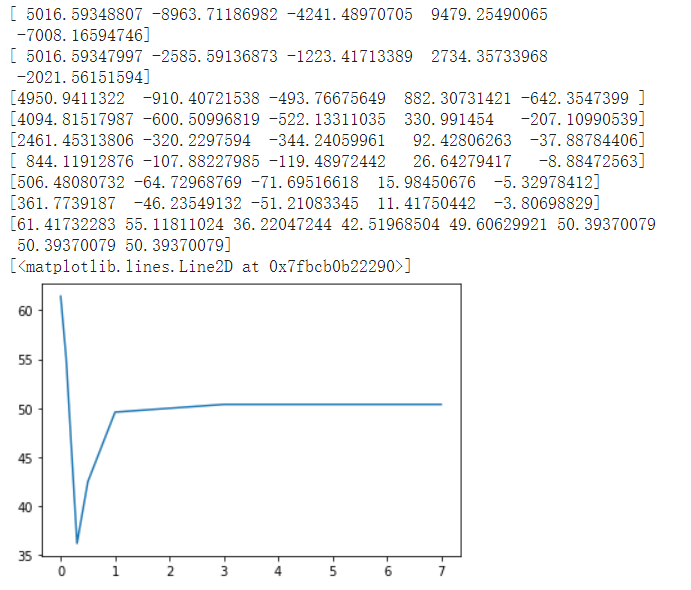
image-20211020121145028

因为更改lambda超参数重新训练模型花费的时间较长，我也尝试了另一种方法：不套sigmoid函数来得到它的概率值而是采用长度比例将其归一化。（不知道这种方法是否正确）

采用的是

这种方法依赖于验证集，修改阈值后是否能在真实数据中表现好？因为采用的是排序切分的方法，一定会有百分之多少的数据进入正例，那么就要求训练集测试集中正例反例的比例要符合现实情况。

使用

1
2
GD_y_predict = sigmoid(GD) > 0.5
NT_y_predict = sigmoid(NT) > 0.5

时，得到的正确率为：

image-20211019151232762

改为

1
2
GD_y_predict = sigmoid(GD/(GD_max-GD_min) * 6) > 0.5
NT_y_predict = sigmoid(NT/(NT_max-NT_min) * 6) > 0.5

后，结果一致，证明正确：

image-20211019151350886

且此时得出的predict值为预想中的概率值：

image-20211019151438989

留言

⬆︎TOP