KMP字符串匹配算法图解

KMP算法是字符串匹配算法中对暴力匹配算法的优化。我尽量用容易理解的方法把它写 & 画清楚。

BF

暴力破解。这是最朴素的一种解决方案：从文本串（即被匹配的大字符串，以下都是）的第一个字符开始，一位一位地与模式串（即搜索的关键字，以下都是）的对应位置相比较。

暴力算法

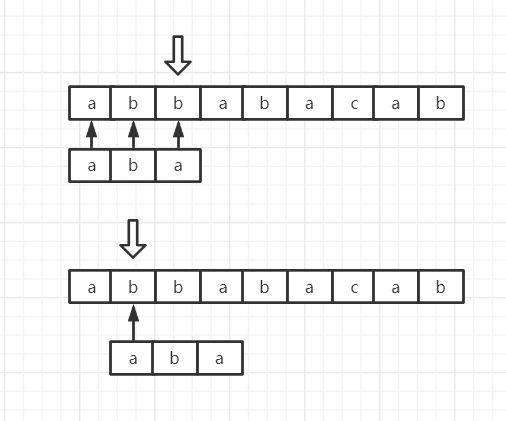
设文本串(p)的长度为m，模式串(s)的长度为n。i，j分别是指向文本串、模式串的游标。

while（i < m) {

​ if (p[i] != s[j]) {

​ i++; j = 0;

​ } else {

​ i++; j++;

​ }

}

但可想而知，这样的匹配算法时间复杂度几乎为O(mn)。但仔细想想，我们确实没必要再比较上图中第二步的a与b，因为在第一步已经比较到了文本串的b，我们应该让程序“记住”它比较过了的东西，在明显与模式串的第一个字符不相同后，就应该去掉第二步。

但我们不能真的去把之前比较过的数据保存起来，那样既增加了空间开销，又没能达到优化的目的。于是，KMP就要登场了，它能帮程序不用像傻子一样（虽然它就是）一个一个地比较下去。

KMP

思想

有一种巧妙的方法。因为假设比较到第k位就失配了（崩了），那么有一个事实是可以确定的：两个串前k-1个字符肯定是相同的。那么！因为模式串是已经定好的，在匹配到j == k时停下来，我们（程序）就知道在文本串中 [i-j, i-1]的字符是什么了。那么知道了以后呢？我们的目的是不要像暴力算法那样一个个比，那就得跳过一些，但又不能把能匹配得上的给跳过了，那么我们就需要看已知的（已经比较过的）文本串中有没有跟模式串开头相同的字符（串）了。没有的话就可以直接跳过前j个，有的话就跳到相同的那一部分继续往下比较。

这里面有一个小点，既然我们已经知道其中有连续的几个是与模式串的前缀（即前面连续的几个）是相同的，那么也没必要再比较了，直接从文本串中程序“未知的”那一个位置继续下去。

如下图，前面三个aba已知，同时模式串a又能与aba中第二个a匹配，那么就直接把模式串移到模式串开头的a与aba中第二个a匹配的位置，同时把模式串的游标j移到a后面的b，从它开始比较。

KMP

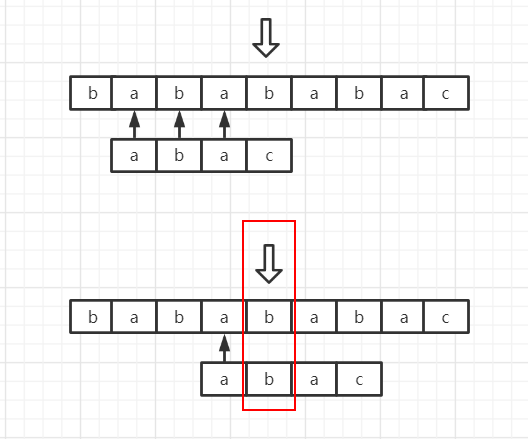
可是，问题又来了。怎么要让程序知道应该跳过其中的多少步呢？

这就又要归功于模式串的已知和不变了，我们现在的任务是什么？我们现在的任务就是在一段已知的字符串（即已经比较过的那一段，也即模式串的一个前缀，上图中的aba）中找是不是有（它的）前缀后缀相同的地方啊。如上图，前后缀相同的就是a。

相同有什么用呢？因为我们要找相同的这一段恰好就是模式串的前缀，且我们是在这一段字符的下一个字符失配的，我们找到这一个字符串中后面某几位是否与前面的某几位相同，就可以知道这里面有没有我们需要移动模式串的位置再匹配一下的地方了。

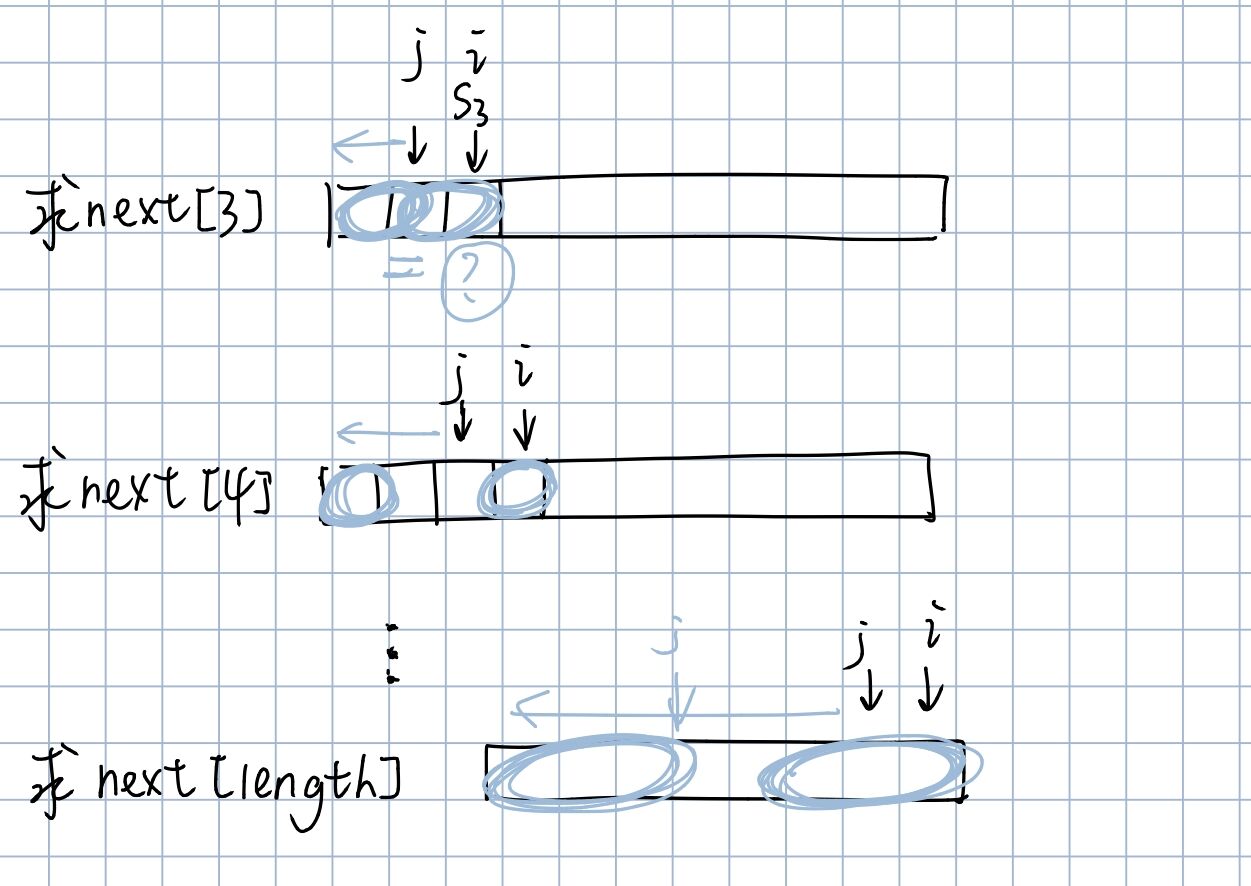
那么，我们可以针对模式串建立一个数组 next[]。next[m]里面存储的是若在（模式串）第m位失配，下一次比较中模式串的游标应该要指向的位置。文本串的游标不变。当需要用到next[i]时，说明前面i-1个字符都是匹配的，到了第i个不相同，那么就需要在前i-1个字符组成的字符串中找是否有相同的前后缀。

代码

由此可以写出kmp基本代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private static int kmp(String p, String s) {
    if(s == null || s.length() == 0) return -1;
    int[] next = new int[s.length()];
    //initNext1(s, next);
    initNext2(s, next);
    int i=0, j=0;
    while(i<p.length() && j<s.length()) {
        if(p.charAt(i) == s.charAt(j)) {
            i++;
            j++;
        } else if (j == 0) {  
            // 因为将next[0]设置为-1，代表需要移动文本串游标
            // 因此需要将j==0的情况单独抽离出来，防止下标越界（j被赋值为-1）
            i++;
        } else {
            j = next[j];
        }
    }
    if(j == s.length()) return i - j + 1;
    return -1;
}

initNext（生成next数组）有两种方法：数学归纳法和先前搜索法。

生成next数组

将next[0]设置为-1，代表需要移动文本串游标。若设置为0，则在第一个字符就失配的情况下会陷入死循环。next[1] = 0：若第二个字符失配，则将模式串向后移1位，即游标指向0，从头开始。

数学归纳法

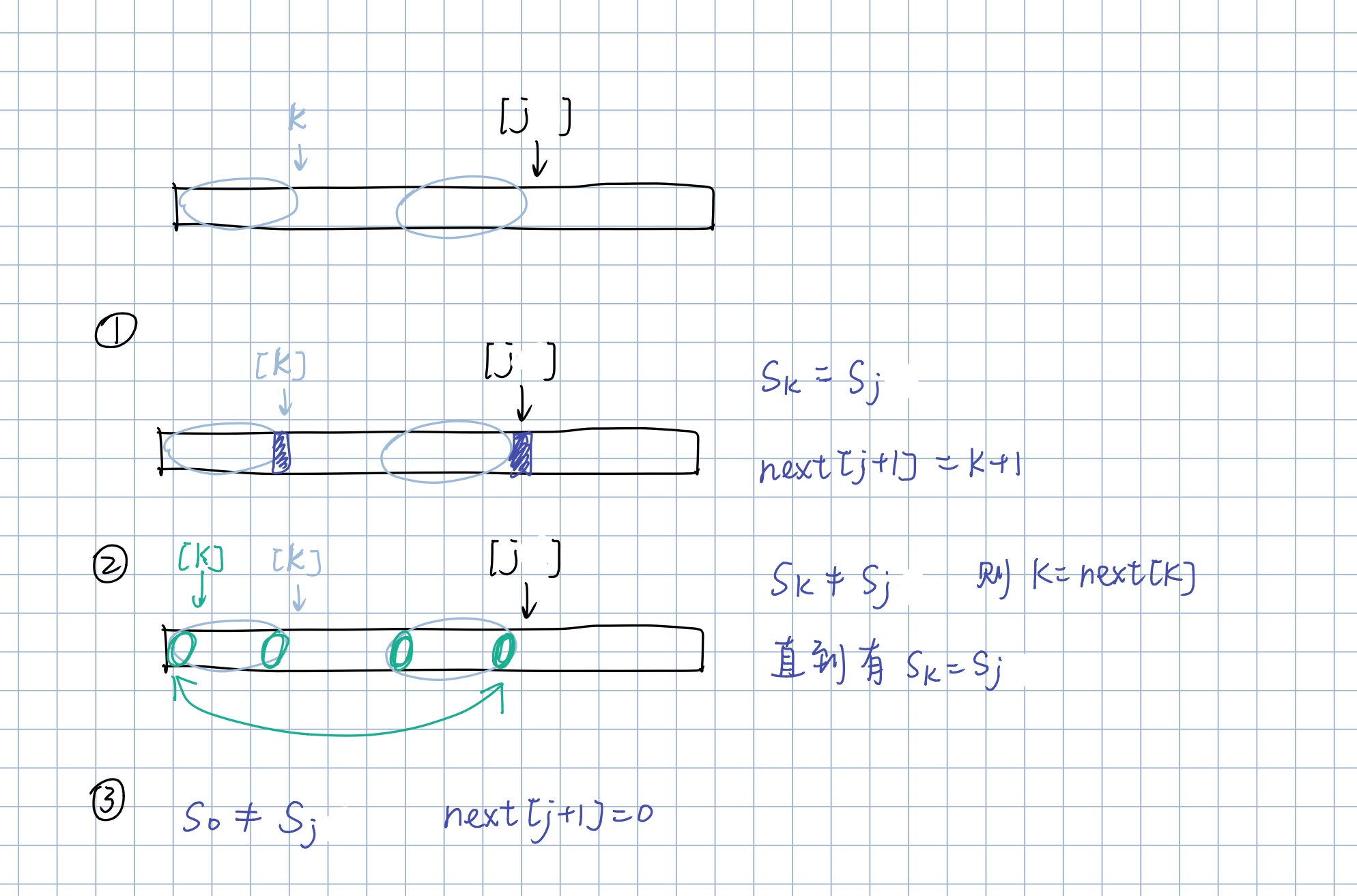
假设next[j]已知，求出next[j+1]的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
   * 生成next数组（数学归纳法）
   */
private static void initNext1(String s, int[] next) {
    next[0] = -1;
    if(next.length == 1) return;
    int j = 1, k = next[j];  // next[0]已经确定，从next[1]开始生成，j=1
    while(j + 1 < next.length) {  // 确定j后面还有字符（存在失配可能）
        while(k != -1) {
            if(s.charAt(j) == s.charAt(k)) { 
                next[j+1] = k + 1;   // k=next[j]
                break;
            } else {
                k = next[k];
            }
        }
        if(k == -1) next[j+1] = 0;  // 说明S0 != Sj
        j++;
        k = next[j];
    }
}

next

向前搜索法

朴素解法。从前缀 & 后缀的后面开始比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
   * 生成next数组（向前搜索）
   */
private static void initNext2(String s, int[] next) {
    if(next.length == 1) {
        next[0] = -1;
        return;
    }
    next[1] = 0;
    for(int i=2; i<s.length(); i++) {
        for(int j=i-1; j>=0; j--) {
            boolean find = true;
            if(s.charAt(i) == s.charAt(j)) {
                int i1 = i, j1 = j;
                while(j1 >= 0) {
                    if(s.charAt(i1) == s.charAt(j1)) {
                        i1--;
                        j1--;
                    } else {
                        find = false;
                        break;
                    }
                }
                if(find) {
                    next[i] = j;
                    break;
                } else continue;
            }
            if(j == 0) next[i] = 0;
        }
    }
}

next2

留言

⬆︎TOP